论文信息
IIRC: Incremental Implicitly-Refined Classification
- 会议:CVPR 2021
- 作者:蒙特利尔大学等
本文最主要的贡献就是提出的持续学习新场景:IIRC (Incremental Implicitly-Refined Classification),文章也围绕此场景:
- 形式化定义此场景;
- 提供了Benchmark,以供模型在此场景的评估;
- 实验评估已有的经典持续学习模型在此场景上的表现。
这个 IIRC 与导师提给我的一个具体场景相像,算是涉及粗细标签的基础场景,值得仔细研究。
当持续学习遇上粗细分类
持续学习已有很多流行的场景,如任务增量学习、类别增量学习,目前大部分持续学习模型都是在这几个流行场景的 benchmark 上测试的。类别增量学习应该是最流行的,即一个任务来一整个(或多个)类的数据。
这个场景是假定了各任务的类别标签在语义上是同一层级的。但如果来的几个类有粗细的包含关系(本文只研究这种关系),那就有意思了。例如,第一个任务学“熊”类,第二个任务学“北极熊”类,这种包含关系的信息,模型从哪儿得知呢?只能从数据里找规律了:但是现在不仅要像原来那样学到两个类的区别,还要学到两个类的联系。
让模型自己通过训练去找这种包含关系显然是为难它了。何不直接告诉它,这两个类是有包含关系的呢?也就是说,喂给模型的某些数据里就显示地表明了类之间的包含关系。 最直观的做法是对数据的结构作扩展:同一个数据允许用多个由粗到细的标签来反复使用。举个例子,对同一张熊的照片 \(\mathbf{x}\),我允许在第一个任务中使用数据 (\(\mathbf{x}\), “熊”) 来学习粗类“熊“,也允许在后面的任务使用 (\(\mathbf{x}\), “北极熊”) 来学习细类“北极熊“。这是IIRC相较于类别增量学习作的核心改变。
IIRC 形式化定义
每个数据允许有多个粗细的标签,本文限定为两个,分别称为超类(superclass)与子类(subclass)。如果某个标签没有更粗或更细的标签,则认其为子类。
对于任务序列 \(\tau_1, \cdots, \tau_N\),每个任务 \(\tau_k\) 会新来一个或多个类 \(C_{k1}, \cdots, C_{kp_k}\),这个类可以是超类或子类中的某一个。与类别增量学习一样,假设它们没有重复。另外要求,不允许在之前任务没有涉及对应的超类的情况下,出现子类。(也排除掉了同一个任务同时出现超类和子类的情况。)这样的话,第一个任务出现的只能都是超类。
打个比方,如果把整个任务序列中涉及的类放到表格里,对于每个任务,类别增量学习就是从下面一个一维表格中不重复地选几个类:
| Bear | Bus | Dog | Lamp | Bird | Truck |
IIRC则从二维表格中不重复地选,但必须先把超类选掉,才能解锁它的子类。
| Bear | Bus | Dog | Lamp | Bird | Truck |
| Polar Bear | Minibus | Whippet |
对于第 \(k\) 个任务的模型 \(f_k\):
- 训练阶段只能看到训练数据的这一个类标签 \(C_{k1}, \cdots, C_{kp_k}\);
- 但是要求此模型能准确预测出这些类以及(如果这个类是子类的话)各自的超类,因此测试阶段的测试数据标签是同时包含这些类以及(如果这个类是子类的话)各自的超类的。
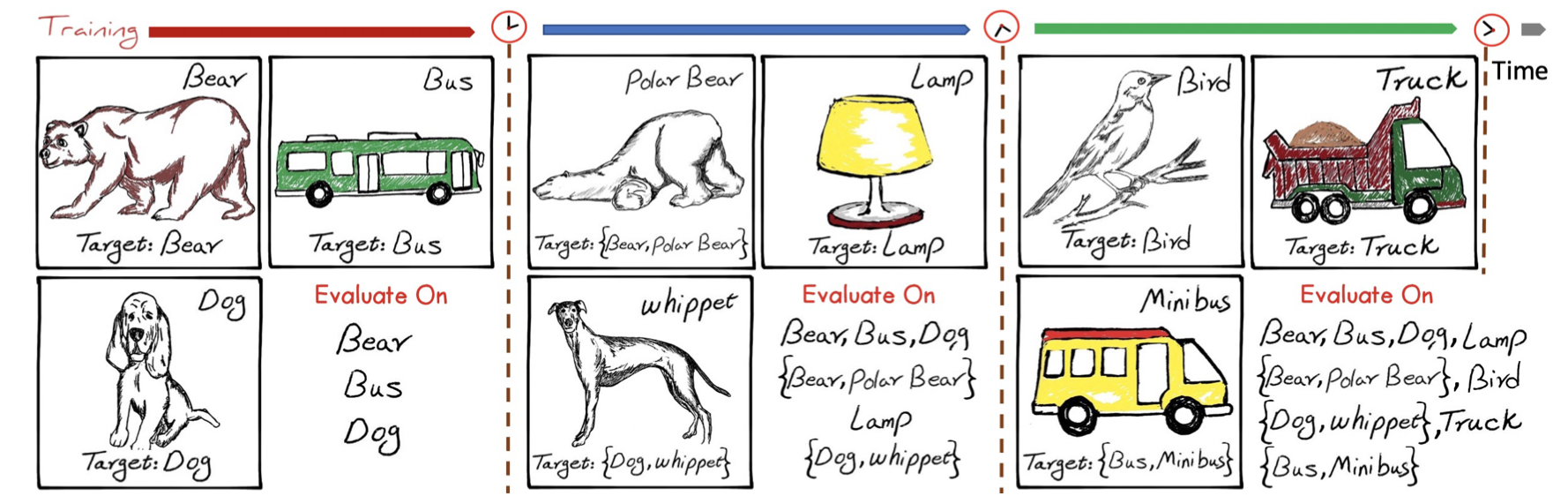
上图是一个例子,展示了 \(N=3\) 个任务,每个框框表示此任务要学习的一个类。右上角表示该类(可见有超类也有子类),也是训练数据只能看到的标签;下方的 Target 表示模型预测的目标(可见已包含子类的超类)。评价模型时,需要计算每个任务的评价指标,每个任务右下角“Evaluate On”展示了这一信息,可见对于子类来说,既要评价是否正确分到子类上,还要评价是否正确分到超类上。
Benchmark
数据集:IIRC-CIFAR、IIRC-ImageNet
作者将 CIFAR100 与 ImageNet 数据集加以改造,得到了这两个适用于 IIRC 场景的数据集。在代码上,就是在构造Dataloader时加了一些预处理。
首先要将类别分成两层(超类、子类)的关系。CIFAR100自带了超类与子类;而ImageNet里的类别层级关系非常庞大,有远大于2层的层级关系,作者是采用了自己的一套标准压缩成2层类别的。
这样就可以了吗?No!上面说了要想子类出场必须先解锁超类,但是目前数据都是划到第2层的子类的,需要拨一些给它们的超类使用。如何拨、拨的比例都在文中给出,不再详述。
评价指标:pw-JS
对于一个输入 \(\mathbf{x}_i\),IIRC 场景下模型预测结果可能不再只输出一个类标签了,而可能是1-2个类标签,记为集合 \(\hat{Y}_i\):
- 1个标签:必须是超类,指属于此超类,且不属于它的任何子类;
- 2个标签:指属于超类下的子类。
真实标签也可能是1-2个标签,同上,记为集合 \(Y_i\)。
评价指标不再是0-1准确率,而应基于这两个集合的关系。作者给出的评价指标称为准确率加权的Jaccard相似度(pw-JS):
\[R=\frac{1}{n} \sum_{i=1}^{n} \frac{\left|Y_{i} \cap \hat{Y}_{i}\right|}{\left|Y_{i} \cup \hat{Y}_{i}\right|} \times \frac{\left|Y_{i} \cap \hat{Y}_{i}\right|}{\left|\hat{Y}_{i}\right|}\]其中第一个因子为 Jaccard 相似度,第二个因子为准确率。对于只有2层类别的 IIRC 场景,其实可以把所有情况穷举出来,列到下面这个表里:
| 例子:\(\hat{Y}_i\) VS \(Y_i\) | 描述 | Jaccard相似度 | 准确率 | 结果 |
|---|---|---|---|---|
| 均为{Bear} 或 均为{Bear, Polar Bear} | 预测完全正确 | \(1\) | \(1\) | \(1\) |
| {Bear} VS {Bear, Polar Bear} | 预测粗了 | \(\frac12\) | \(1\) | \(\frac12\) |
| {Bear, Polar Bear} VS {Bear} | 预测细了 | \(\frac12\) | \(\frac12\) | \(\frac14\) |
| {Bear, Polar Bear} VS {Bear, Brown Bear} | 细类预测错了 | \(\frac13\) | \(\frac12\) | \(\frac16\) |
| {Bear, (随意)} VS {Dog, (随意)} | 粗类预测错了 | \(0\) | \(0\) | \(0\) |
可以看到,这个指标有一个致命的问题。假设模型已经将粗类预测正确,那么它现在有两个选择:继续预测细类/不预测细类。观察上表,可以看到:预测成功的收益都是1;前者预测错误即预测细了收益为 \(1/4\),是小于后者预测错误即预测粗了的收益 \(1/2\)的。所以,一个聪明的模型会发现,那些努力的人(预测细了)得不到表扬,费力不讨好,还不如偷懒(往粗了预测)呢!虽然这个指标没有加到损失函数里参与到了模型的训练中,但这个指标确实是不科学、不公平的。
实验
已有的经典持续学习模型如何套到IIRC场景中?实际上此场景只是把普通的多分类改为了多标签分类。处理方法很简单,只需将最后一层 Softmax 分类器改为多个 Sigmoid 分类器,分类损失选择二分类损失(BCE)即可。
实验为测试经过改造的经典持续学习模型在本文 Benchmark 上的表现,不再展示。