首页 PyTorch 学习笔记（四）：深度学习的训练
文章
取消

PyTorch 学习笔记（四）：深度学习的训练

作者 Shawn Wang
发表于 2022-02-11 更新于 2023-05-27 20 分钟阅读

本文总结 PyTorch 是如何实现深度学习训练中的各种技巧与细节，包括防止过拟合、参数初始化、优化器、损失函数、超参数优化等等。关于这部分知识，我在这篇笔记中有系统的总结。本文的编排顺序基本与这篇笔记对应（数据预处理部分在介绍 Dataset 类型的笔记中，调参、学习曲线等放在 PyTorch 工程性知识的笔记中）。此外，还有一篇笔记总结了深度学习训练的实践经验，可供参考。

本文参考 Dive into Deep Learning (PyTorch 版) 中的以下内容：

  • 4.4 节：模型选择、欠拟合与过拟合；
  • 4.5 节：权重衰减；
  • 4.6 节：暂退法；
  • 4.8 节：数值稳定性与模型初始化；
  • 4.9 节：环境和分布偏移；
  • 第 11 章：优化算法

一、激活函数

激活函数在形式上应该是一个 Python 函数，它接受 Tensor 类型的输入并输出相同维度的 Tensor 变量。在笔记（一）MLP 的从头开始实现中可以看到：

1
2
3

def relu(x):
    a = torch.zeros_like(x)
    return torch.max(X, a)

在 torch.nn.functional 中有各种预定义的激活函数，见文档：https://pytorch.org/docs/stable/nn.functional.html#non-linear-activation-functions

torch.nn.functional 提供了各种深度学习可能用到的预定义函数。这里都是用 Python 函数实现的，相对来说封装程度没有那么高，一般用于自己模型设计的零件；下面可以看到，很多这种函数如激活函数、损失函数是实现为一个可调用类的，封装程度更高。

在深度学习中，激活函数的用处就是作为 nn.Module 模型的一个组成部分。使用的方法就是将其套在 forward 函数中。以下是笔记（三）自定义块中见到的例子：

1
2
3
4
5
6
7

class MLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(784, 256)
        self.out = nn.Linear(256, 10)
    def forward(self, X):
        return self.out(nn.functional.relu(self.hidden(X)))

因此在实际使用 PyTorch 的高级 API 中，激活函数被看成是一个层，是 nn.Module 类型。我们也在笔记（三）自定义层中见到过：

1
2
3
4
5

class ReLULayer(nn.Module):
    def __init__(self):
        super().__init__()
    def forward(self, X):
        return nn.functional.relu(X)

当然 PyTorch 也预定义了很多这种激活函数层，它们放在 torch.nn 中（文档），与其他预定义的有实际参数的层（如 nn.Linear）并列。这种预定义层的用法就是放在 nn.Sequential 容器里，与其他层串联。例如，上述自定义层等价于如下预定义层：

1

relu = nn.ReLU()

三、网络结构

注：“二、数据预处理” 我放到了笔记（二）中，和对 Dataset 的介绍放在了一起。下面从 “三、网络结构” 开始。

对网络结构下手的一些训练 trick 与 nn.Module 是兼容的，可以看作一种特殊的层。PyTorch 为 Dropout 和 Batch Normalization 都提供了高级的 API：nn.Dropout()、nn.BatchNorm1d()。对于图像等数据，还提供了 2D、3D 等版本。

这里需要注意的是，Dropout 和 Batch Normalization 都是训练和测试不一样的层（在训练阶段引入随机性，在测试阶段以期望值代替来消除随机性），所以这些层前向传播时，必须要有指示告诉它们是训练还是测试。PyTorch 设计了这个指示变量封装在 nn.Module 类型的实例属性 training 中（布尔变量）；方法 .train() 与 .eval() 可以修改此变量，把它放在整个训练或测试阶段开始前即可。

四、参数管理与初始化

这节的内容是参数初始化，我会连带讲解 PyTorch 的模型参数管理机制，即与 nn.Module 对象定义的模型参数有关的操作。

笔记（一）的最后一个模型已经看到，nn.Module 的模型参数都属于 nn.Parameter 类。这是一个封装模型参数的类（文档），将其与普通的 Tensor 区别开，便于训练和管理（我们在以后可以看到封装的优势）。此类在构造时接受两个参数：

  • data：参数数据，Tensor 或 nn.Parameter 类型（允许递归嵌套）；它直接构造了实例属性 .data，要直接取得 nn.Parameter 类封装的 Tensor，应访问该实例属性；
  • requires_grad：指定 data 是否需要梯度。

当然，参数指的是模型参数，是与模型挂钩的，一般不单独实例化 nn.Parameter 对象，而是在模型 nn.Module 实例化时就已经存在了。笔记（一）的最后一个模型只是起了演示的作用。

访问模型的参数

6

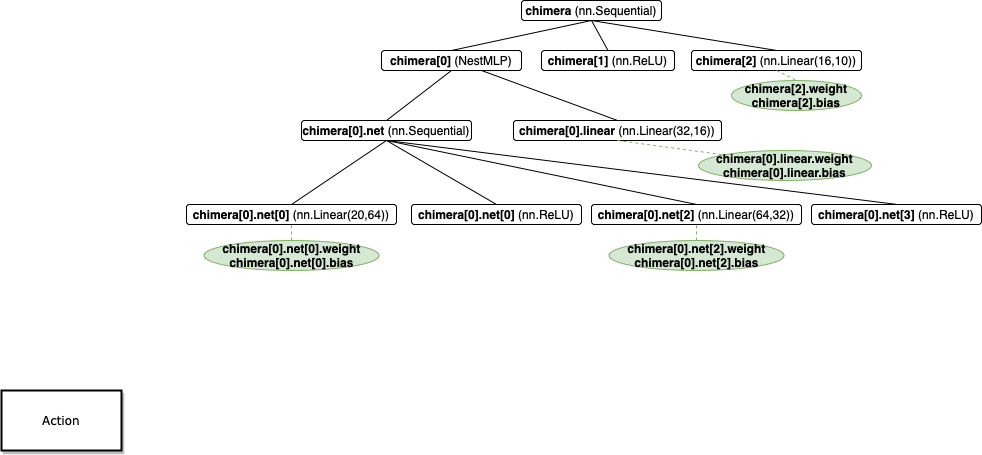
模型的参数应该是模型的一个属性。上图是笔记（三） NestMLP 的参数图（它与笔记（三）图的区别在于，有参数的层外挂了一个绿色的叶子结点）。可以看到参数放在了模型的 weight、bias 属性中。

因此，访问模型某层的参数可以直接按照图中绿色叶子结点的调用方式。

PyTorch 也设计了访问模型所有参数的方法，注意，在 nn.Module 类中定义的所有 nn.Parameter 的实例属性都被视为模型参数（不管它是否参与到 forward 函数）。与 nn.Module 同理，其算法也是递归地遍历树的叶子。API 有：

  • .parameters() 方法：返回一个生成器。这种方式访问通常用于直接传入优化器的 params 参数，print 无法直接显示，需要遍历其元素 print（或者强制转化为列表）；
  • .named_parameters() 方法，返回生成器生成的是 (参数名字, 参数数据) 对。参数的命名空间与模型一致；
  • .state_dict() 方法：返回一个 collections.OrderedDict 类型，字典键值为 {参数名字:参数数据}， print 可以显示。

参数初始化

这里讨论封装在 nn.Parameter 中的参数的初始化。

参数初始化当然也可以直接取出 data 属性，对其赋值或修改。但更好用的是能直接对 nn.Parameter 对象作初始化的修改函数，这也是封装 nn.Parameter 的意义。PyTorch 提供了很多初始化函数，它们作用在 nn.Parameter 对象上。这些函数定义在 nn.init 模块中，以下列举几个常用的，其他的详见文档：https://pytorch.org/docs/stable/nn.init.html。

  • nn.init.normal(tensor, mean, std)：从正态分布 \(N(mean, std)\) 初始化
  • nn.init.constant(tensor, val)：全部以常量 val 初始化
  • nn.init.uniform(tensor, a, b)：从均匀分布 \(U(a,b)\) 初始化
  • nn.init.xavier_uniform(tensor, gain), nn.init.xavier_normal(tensor, gain)：Xavier 初始化
  • nn.init.kaiming_uniform(tensor, a, mode), nn.init.kaiming_normal(tensor, a, mode)：何恺明的初始化

当然，这些函数内部细节就是取出 data 属性后对 Tensor 的操作，也可以自己按照的方式定义一个初始化函数。

PyTorch 预定义的 nn.Module 层带有默认的初始化方法（reset_parameters()），是一些优秀初始化方法的汇总和精调，在实例化模型时就会调用它。PyTorch 为每种层都涉及了适合它们的默认初始化方法。 因此，除了研究不同初始化方法的需要，在高级 API 搭建深度学习模型的流程中可以省略初始化这一步。

在实际中，参数初始化一般是整体地对一整个模型初始化。通常是打包成一个 init_parameters 函数，通过 nn.Module 的 apply 方法（可以将传入的函数递归地作用到它包含的所有层上）作用到模型参数上。以下是[笔记（一）]中出现的例子：

1
2
3
4
5

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

可以看到，一个函数也能搞定对不同层的不同初始化，只要加 if 规则判断就行。这样打包成一个函数的好处是方便维护代码。

对于预训练模型用别人训好的参数作初始化，涉及模型的读写文件，见这一篇笔记，不在这里讲。

五、优化器

优化器就是一个对参数的修改函数，它接受待更新的参数，利用参数中存储的梯度信息（见笔记（一）自动微分部分，计算的梯度存放在参数 Tensor 的 grad 属性中，因此不需要传梯度参数），在函数主体中完成对参数的一步更新（如梯度下降法）。最后要有一步梯度清零的操作，也是在这里实现的。还要注意这部分代码要用 with torch.no_grad(): 包裹，这些在笔记（一）中都提到了。

一个优化器函数形式如下：

1
2
3
4
5
6

def optimizer(params, hyperparams):
    with torch.no_grad():
        for p in params: # 遍历模型参数
            g = p.grad # 提取梯度
            ... # 对 p 的修改，是基于 g 的公式
            p.grad.zero_()

其中的超参数除学习率外可能还有很多，为了形式统一，往往打包成字典的形式，在用的时候取字典值。例如动量法传入的超参数形式为 {'lr':lr, 'momentum':momentum}。

之前实现的是随机梯度下降（SGD），相对比较简单，只需用一下梯度下降公式即可。更复杂的优化器如 Momentum、AdaGrad、Adam 等，往往需要维护一组状态值，它们随着训练过程也像参数一样进行迭代，且需要初始化。这种状态值的处理也很简单，可以放在全局变量或优化器函数的参数里，不再赘述。

实际上在 PyTorch 中，优化器并不是简单的修改函数，而是继承的 torch.optim.Optimizer 类，这样有利于提供更完整、健全的优化器功能，例如设置默认值等，PyTorch 提供的 API 也都是 Optimizer 类型，详见文档；对参数的修改定义在 step() 方法里。自己写优化器时，如果有需求，可以按这种方式写比较复杂的类（但写成函数基本就够用了）：

1
2
3
4
5
6
7
8

class MyOptimizer(torch.optim.Optimizer):

    def__init__(self, params, hyperparams):
        ...

    @torch.no_grad()
    def step(self, closure=None):
        ...# 对 self.params 的修改，梯度清零等

PyTorch 提供了方便的优化器 API，在 torch.optim 中（文档：https://pytorch.org/docs/stable/optim.html#algorithms），在搭建项目时，如无特殊需求，也不必自己写优化器：

  • torch.optim.SGD：实现了 SGD、SGD + Momentum；
  • torch.optim.Adagrad、torch.optim.RMSprop：实现了 AdaGrad、RMSProp；
  • torch.optim.Adam、torch.optim.AdamW：实现了 Adam 及其一些改进算法。

学习率调整器

上述每个优化器都有学习率超参数，都可以设计学习率调整策略。学习率调整就是在训练过程中不断地改变学习率，这样看的话学习率就类似于一种参数。PyTorch 将学习率看做了一种参数，设计了专门针对这个“参数”的优化器——学习率调整器（learning rate scheduler），放在 torch.optim.lr_scheduler 中。

它的使用方法与 Optimizer 类似，但也有一个重要的区别（这也是为什么单独设计一个类的原因）：lr_scheduler 类传入的不是超参数，而是优化器，以指数衰减调整器为例，它的实例化：

1
2
3
4

from torch.optim.lr_scheduler import ExponentialLR

optimizer = SGD(model, 0.1)
scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.9)

这样是为了不想让学习率裸露在训练过程外面，而是始终与优化器捆绑在一起，为了代码的模块化。

如果不是专门研究学习率，PyTorch 提供的 API 就够用了（见文档），这种东西用的不多，也几乎没有需要自己写的场合，所以知道有这种东西就差不多了。

六、损失函数

损失函数在形式伤也是一个 Python 函数，它接受数据预测值和真实值的 Tensor 类型的输入并输出一个数。在笔记（一）MLP 的从头开始实现中可以看到：

1
2

def squared_loss(y_hat, y):
    return (y_hat - y) ** 2 / 2

在 torch.nn.functional 中也有各种预定义的损失函数，见文档：https://pytorch.org/docs/stable/nn.functional.html#loss-functions

与激活函数类似，损失函数也被 PyTorch 的高级 API 实现为一个 nn.Module 层，它们也放在 torch.nn 中（文档），与其他预定义的有实际参数的层（如 nn.Linear）并列。这里预定义的都是最基本、原始的损失函数，使用方法相对来说比较固定，例如：

  • 交叉熵损失，用于分类问题：nn.CrossEntropyLoss()；
  • 平方损失，用于回归问题：nn.MSELoss()；
  • …

在深度学习中，除了原始的损失函数，还会加正则项，实现其他目的，如防止过拟合、迁移学习的迁移、持续学习的防遗忘等。

实现正则项的方式是自由的，可以与原始损失函数打包到一个 nn.Module 类（用 forward 函数嵌套的原理）或 Python 函数，也可以单独写成一个损失函数，在训练过程中计算损失的时候加进来：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class RegLoss(nn.Module):

    def __init__(self, factor):
        ...
        self.factor = factor # 正则化系数

    def forward(self, y_hat, y):
        reg_loss = ... # 使用 y_hat 和 y 定义的公式
        return self.factor * reg_loss

loss = nn.CrossEntropyLoss()
reg = RegLoss(factor=FACTOR)

# 训练过程
for epoch:
    for batch:
        ...
        l = loss(net(X), y) + reg(net(X), y)
        l.backward()
        ...
...

正则化系数可以放在训练过程外面，也可以像上面这样打包到损失函数里面。具体怎么实现，全看代码模块化程度的需要。

值得注意的是 L2 正则化，因为它与修改梯度下降公式的权重衰减等价，除了在损失中实现 L2 正则项，还可以直接在优化器中实现。在 PyTorch 的高级 API 中，大部分优化器提供一个超参数：weight_decay，传入即可实现权重衰减。

科研
PyTorch 读书笔记 《动手学深度学习》 技术
本文由作者按照 CC BY 4.0 进行授权，转载请注明
最近更新
文章内容

PyTorch 学习笔记（五）：计算性能

编配：《钢铁洪流进行曲》手风琴四重奏